8556. Цепь

Дана последовательность из n целых чисел a₁, a₂, ..., a_n. Для каждого элемента a_k (k = 1, 2, ..., n) мы находим первый элемент правее a_k, больший его (если такой существует). Обозначим такой элемент a_k1. Затем сделаем то же самое для элемента a_k1 и обозначим найденный элемент a_k2, и так далее пока последовательность не закончится. Таким образом формируется подпоследовательность a_k1, a_k2, ..., которую мы назовем цепью, начинающейся с индекса k.

Напишите программу, которая выводит для каждого индекса k длину соответствующей цепи, начинающейся с индекса k.

Вход. В первой строке записано натуральное число n (0 < n ≤ 500000). Во второй строке даны элементы последовательности a₁, a₂, ..., a_n (0 < a_i < 10⁶).

Выход. В одной строке выведите последовательность длин цепей, соответствующих элементам входных данных.

Пример входа	Пример выхода
10 3 2 4 2 11 2 7 5 8 10	2 2 1 1 0 3 2 2 1 0

РЕШЕНИЕ

стек

Анализ алгоритма

Объявим массив nex такой что nex[i] содержит индекс ближайшего справа элемента, большего a_i. Например, nex[i] = 0 означает что справа от a_i нет элементов, больших a_i.

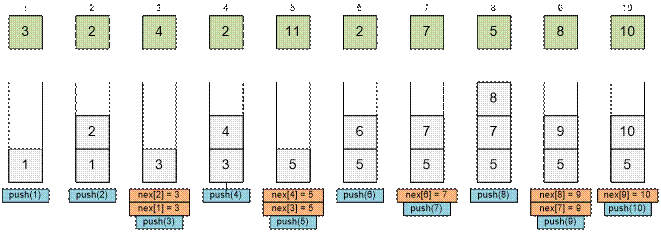
Объявим стек s, который вместо чисел a_i будет хранить индексы i. Занесем в стек первый элемент: s.push(1) – заносим индекс первого элемента. Последовательно обрабатываем остальные числа последовательности. Пусть текущим элементом является a_j. Тогда:

· если a[s.top()] ≥ a[j], то индекс j кладем в стек: s.push(j);

· иначе пока стек не пустой и a[s.top()] < a[j], извлекаем элемент из стека i = s.top() и устанавливаем nex[i] = j. По завершению цикла j заносим в стек: s.push(j);

Теперь по массиву nex следует восстановить результирующую последовательность dp, где dp[i] равно длине цепи, начинающейся с индекса i. Двигаемся с конца массива в начало (i = n, n – 1, …, 2, 1) и вычисляем значение dp[i]:

· если nex[i] = 0, то dp[i] = 0;

· иначе dp[i] = dp[nex[i]] + 1;

Отметим, что для вычисления dp[i] значение dp[nex[i]] уже должно быть найдено, поэтому вычисление ячеек массива dp следует выполнять справа налево.

Пример

Заполняем массив dp справа налево.

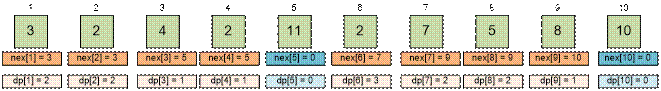
Реализация алгоритма

Объявим рабочие массивы.

#define MAX 500001

int a[MAX], nex[MAX], dp[MAX];

stack<int> s;

Основная часть программы. Читаем входные данные.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Заносим в стек индекс первого элемента – единицу.

s.push(1);

Последовательно обрабатываем остальные элементы.

for(j = 2; j <= n; j++)

{

while(!s.empty())

{

i = s.top();

if(a[i] >= a[j]) break;

nex[i] = j;

s.pop();

}

s.push(j);

}

Пересчитываем результирующий массив.

dp[n] = 0;

for(i = n - 1; i >= 1; i--)

if (nex[i] == 0) dp[i] = 0;

else dp[i] = 1 + dp[nex[i]];

Выводим ответ – длины цепей, начинающихся с позиции i.

for(i = 1; i <= n; i++)

printf("%d ",dp[i]);

printf("\n");

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int a[] = new int[n+1];

int next[] = new int[n+1];

int dp[] = new int[n+1];

for(int i = 1; i <= n; i++)

a[i] = con.nextInt();

Stack<Integer> s = new Stack<Integer>();

s.push(1);

for(int j = 2; j <= n; j++)

{

while(!s.empty())

{

int i = s.peek();

if(a[i] >= a[j]) break;

next[i] = j;

s.pop();

}

s.push(j);

}

dp[n] = 0;

for(int i = n - 1; i >= 1; i--)

if (next[i] == 0) dp[i] = 0;

else dp[i] = 1 + dp[next[i]];

for(int i = 1; i <= n; i++)

System.out.print(dp[i] + " ");

System.out.println();

con.close();

}

}